I’m working on OpenMP parallelization of a lattice Boltzmann kernel for a 2D periodical domain.
The full streaming kernel (lacking a few module constants) is in the details box:
Full kernel
subroutine kernel_stream(nx,ny,ld,ft,fp,dt,omega)
integer, intent(in) :: nx, ny, ld
real(wp), intent(in) :: ft(ld,nx,0:8) ! \bar{f}^{+,n}
real(wp), intent(inout) :: fp(ld,nx,0:8) ! \tilde{f}^{+,n}
real(wp), intent(in) :: dt, omega
real(wp) :: cfw(ny,0:8), cfn(ny,0:8)
real(wp) :: cfrho(ny), cfux(ny), cfuy(ny), cfindp(ny)
real(wp) :: fc, fe, fn, fw, fs, fne, fnw, fsw
real(wp), parameter :: p2 = 0.5_wp, &
p8 = 0.125_wp
integer :: x, y, q
integer :: xp1, xm1, yp1, ym1
real(wp) :: cxq, cyq
real(wp) :: fluxW, fluxN
!$omp parallel default(private) shared(nx,ny,ld,ft,fp,dt,omega)
!$omp do schedule(static)
do x = 1, nx
! locate neighbor nodes
xp1 = mod(x, nx) + 1
xm1 = mod(nx + x - 2, nx) + 1
! Interpolate values at the WEST and NORTH cell faces
!
! All directions are needed, so we can calculate the
! macroscopic values
!
do q = 0, 8
cxq = dt*cx(q)
cyq = dt*cy(q)
do y = 1, ny
yp1 = mod(y, ny) + 1
ym1 = mod(ny + y - 2, ny) + 1
! read pdf values
fc = ft(y , x , q)
fe = ft(y , xp1, q)
fn = ft(yp1, x , q)
fw = ft(y , xm1, q)
fs = ft(ym1, x , q)
fne = ft(yp1, xp1, q)
fnw = ft(yp1, xm1, q)
fsw = ft(ym1, xm1, q)
! fse = ft(ym1, xp1, q) ! not needed
! West cell face
cfw(y,q) = p2*(fc + fw) - p2*cxq*(fc - fw) - &
p8*cyq*(fnw + fn - fsw - fs)
! North cell face
cfn(y,q) = p2*(fc + fn) - p2*cyq*(fn - fc) - &
p8*cxq*(fne + fe - fnw - fw)
end do
end do
! Update values at cell faces
!
! cf = (1 - omega)*cf + omega * cfeq
!
#if DUGKS
! WEST face
call update_ew(ny,cfw,cfrho,cfux,cfuy,cfindp,omega)
! NORTH face
call update_ns(ny,cfn,cfrho,cfux,cfuy,cfindp,omega)
#endif
! TODO:
! At the WEST face we only need to update
! velocites 1,3,5,7,6,8
! At the NORTH face, we only need to update
! velocities 2,4,5,7,6,8
!
do q = 1, 8
cxq = dt*cx(q)
cyq = dt*cy(q)
do y = 1, ny
yp1 = mod(y, ny) + 1
ym1 = mod(ny + y - 2, ny) + 1
fluxW = cxq*cfw(y,q)
fluxN = cyq*cfn(y,q)
!
! WARNING: This section could potentially show a race condition
!
fp(y,x,q) = fp(y,x,q) + fluxW - fluxN
fp(y,xm1,q) = fp(y,xm1,q) - fluxW
fp(yp1,x,q) = fp(yp1,x,q) + fluxN
end do
end do
end do
!$omp end do
!$omp end parallel
contains
subroutine update_ew(ny,f,rho,ux,uy,indp,omega)
integer, intent(in) :: ny
real(wp), intent(inout) :: f(ny,0:8)
real(wp), intent(inout) :: rho(ny), ux(ny), uy(ny), indp(ny)
real(wp), intent(in) :: omega
integer :: y
real(wp) :: invrho
real(wp) :: omegabar, omega_w0, omega_ws, omega_wd
real(wp) :: vel_trm_13, vel_trm_57, vel_trm_68
real(wp) :: velxpy, velxmy
omegabar = 1.0_wp - omega
omega_w0 = 3.0_wp * omega * w0
omega_ws = 3.0_wp * omega * ws
omega_wd = 3.0_wp * omega * wd
do y = 1, ny
rho(y) = (((f(y,5) + f(y,7)) + (f(y,6) + f(y,8))) + &
((f(y,1) + f(y,3)) + (f(y,2) + f(y,4)))) + f(y,0)
invrho = 1.0_wp/rho(y)
ux(y) = invrho * (((f(y,5) - f(y,7)) + (f(y,8) - f(y,6))) + (f(y,1) - f(y,3)))
uy(y) = invrho * (((f(y,5) - f(y,7)) + (f(y,6) - f(y,8))) + (f(y,2) - f(y,4)))
indp(y) = one_third - 0.5_wp * (ux(y)**2 + uy(y)**2)
end do
do y = 1, ny
vel_trm_13 = indp(y) + 1.5_wp * ux(y) * ux(y)
f(y,1) = omegabar*f(y,1) + omega_ws * rho(y) * (vel_trm_13 + ux(y))
f(y,3) = omegabar*f(y,3) + omega_ws * rho(y) * (vel_trm_13 - ux(y))
end do
do y = 1, ny
velxpy = ux(y) + uy(y)
vel_trm_57 = indp(y) + 1.5_wp * velxpy * velxpy
f(y,5) = omegabar*f(y,5) + omega_wd * rho(y) * (vel_trm_57 + velxpy)
f(y,7) = omegabar*f(y,7) + omega_wd * rho(y) * (vel_trm_57 - velxpy)
end do
do y = 1, ny
velxmy = ux(y) - uy(y)
vel_trm_68 = indp(y) + 1.5_wp * velxmy * velxmy
f(y,6) = omegabar*f(y,6) + omega_wd * rho(y) * (vel_trm_68 - velxmy)
f(y,8) = omegabar*f(y,8) + omega_wd * rho(y) * (vel_trm_68 + velxmy)
end do
end subroutine
subroutine update_ns(ny,f,rho,ux,uy,indp,omega)
integer, intent(in) :: ny
real(wp), intent(inout) :: f(ny,0:8)
real(wp), intent(inout) :: rho(ny), ux(ny), uy(ny), indp(ny)
real(wp), intent(in) :: omega
integer :: y
real(wp) :: invrho
real(wp) :: omegabar, omega_w0, omega_ws, omega_wd
real(wp) :: vel_trm_24, vel_trm_57, vel_trm_68
real(wp) :: velxpy, velxmy
omegabar = 1.0_wp - omega
omega_w0 = 3.0_wp * omega * w0
omega_ws = 3.0_wp * omega * ws
omega_wd = 3.0_wp * omega * wd
do y = 1, ny
rho(y) = (((f(y,5) + f(y,7)) + (f(y,6) + f(y,8))) + &
((f(y,1) + f(y,3)) + (f(y,2) + f(y,4)))) + f(y,0)
invrho = 1.0_wp/rho(y)
ux(y) = invrho * (((f(y,5) - f(y,7)) + (f(y,8) - f(y,6))) + (f(y,1) - f(y,3)))
uy(y) = invrho * (((f(y,5) - f(y,7)) + (f(y,6) - f(y,8))) + (f(y,2) - f(y,4)))
indp(y) = one_third - 0.5_wp * (ux(y)**2 + uy(y)**2)
end do
do y = 1, ny
vel_trm_24 = indp(y) + 1.5_wp * uy(y) * uy(y)
f(y,2) = omegabar*f(y,2) + omega_ws * rho(y) * (vel_trm_24 + uy(y))
f(y,4) = omegabar*f(y,4) + omega_ws * rho(y) * (vel_trm_24 - uy(y))
end do
do y = 1, ny
velxpy = ux(y) + uy(y)
vel_trm_57 = indp(y) + 1.5_wp * velxpy * velxpy
f(y,5) = omegabar*f(y,5) + omega_wd * rho(y) * (vel_trm_57 + velxpy)
f(y,7) = omegabar*f(y,7) + omega_wd * rho(y) * (vel_trm_57 - velxpy)
end do
do y = 1, ny
velxmy = ux(y) - uy(y)
vel_trm_68 = indp(y) + 1.5_wp * velxmy * velxmy
f(y,6) = omegabar*f(y,6) + omega_wd * rho(y) * (vel_trm_68 - velxmy)
f(y,8) = omegabar*f(y,8) + omega_wd * rho(y) * (vel_trm_68 + velxmy)
end do
end subroutine
end subroutine
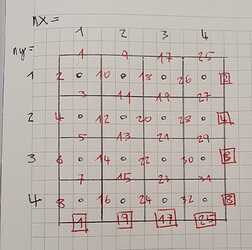
From the numerical point of view, the kernel is a solver for a set of advection equations (q = 0,1,\dots,8) using a finite volume approach on a regular square grid with unit cell length (\Delta x = 1) (the full method is described in this paper). Below is a sketch of a 4×4 grid with numbered cells and edges. The little boxes mark the periodic edge.
To save on evaluations I’m only calculating the fluxes for the west and north faces of each cell. Note that due to the regular structure, I’m not storing an edge list. I’m worried that the marked section where I add/subtract the fluxes from the cell and it’s neighbors presents a potential race condition:
!$omp parallel default(private) shared(nx,ny,ld,ft,fp,dt,omega)
!$omp do schedule(static)
do x = 1, nx
! locate neighbor nodes
xp1 = mod(x, nx) + 1
xm1 = mod(nx + x - 2, nx) + 1
!
! ... interpolation at cell faces ...
!
do q = 1, 8
cxq = dt*cx(q)
cyq = dt*cy(q)
do y = 1, ny
yp1 = mod(y, ny) + 1
ym1 = mod(ny + y - 2, ny) + 1
fluxW = cxq*cfw(y,q)
fluxN = cyq*cfn(y,q)
fp(y,x,q) = fp(y,x,q) + fluxW - fluxN !>
fp(y,xm1,q) = fp(y,xm1,q) - fluxW !> race condition ?
fp(yp1,x,q) = fp(yp1,x,q) + fluxN !>
end do
end do
end do
!$omp end do
!$omp end parallel
To my surprise, for the limited tests that I ran on a 64×64 grid, the results were the same with 1, 4, or 8 threads. I’m guessing I would bump into problems if Edit: I’ve confirmed the results are unreliable, see my second post.nx = 4, and each thread only calculated one column of cells. Then the updates for (y, x) and (y, xm1) (cell to the left) might overlap? For nx = 64 however, I’m guessing the cells are already updated by the time the other threads reach the end of their x section.
Is my understanding correct? Does the cell-face-based loop present a potential race condition? How would a safe cell-face-based update loop look like?