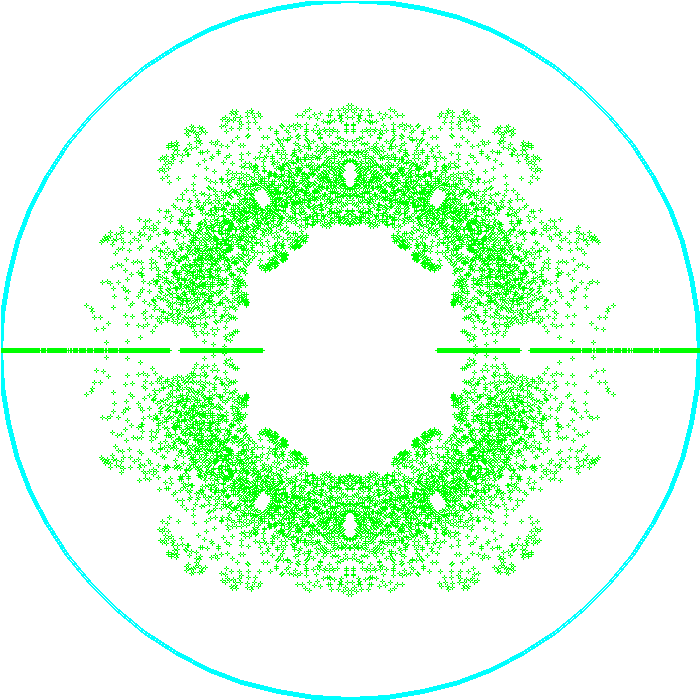
Here’s a little “code golf” exercise. Consider this code:
program polyroots_test_10
use polyroots_module, only: dpolz, wp => polyroots_module_rk
use pyplot_module, only: pyplot
implicit none
integer,parameter :: degree = 10
real(wp),dimension(degree+1) :: a !! coefficients of polynomial
real(wp),dimension(degree) :: zr, zi !! roots
integer :: ierr,i,j,k,l,m,n,o,p,q,r,s
type(pyplot) :: plt
call plt%initialize(grid=.true.,xlabel='$\Re(z)$',ylabel='$\Im(z)$',&
title='Degree 10 Polynomial Roots',usetex=.true.,&
figsize=[20,10])
do i = -1, 1, 2
do j = -1, 1, 2
do k = -1, 1, 2
do l = -1, 1, 2
do m = -1, 1, 2
do n = -1, 1, 2
do o = -1, 1, 2
do p = -1, 1, 2
do q = -1, 1, 2
do r = -1, 1, 2
do s = -1, 1, 2
a = [i,j,k,l,m,n,o,p,q,r,s]
call dpolz(degree,a,zr,zi,ierr); if (ierr/=0) error stop ierr
call plt%add_plot(zr,zi,label='',linestyle='bo',markersize=1)
end do
end do
end do
end do
end do
end do
end do
end do
end do
end do
end do
call plt%savefig('roots.png')
end program polyroots_test_10
The resultant plot can be seen here.
The idea is to get all the combinations where each element of a is either 1 or -1. How can we make this less verbose? Is there an intrinsic way I’m missing, or a library out there somewhere to do this?