Torsten Hoefler’s random access spontaneous talk given at the 42nd anniversary Salishan Conference on High-Speed Computing in 2023. Discusses how to lift Fortran code to a data-centric representation to optimize it for accelerator devices. Work led by Alexandru Calotoiu in SPCL.
For the loop nest at 8:05 Torsten says that not a single compiler can parallelize that loop automatically, but I remain confused if he’s talking about vectorization of the inner loop, or doing the reduction on the outer loop in parallel
The loop appears to be taken out of the dwarf-p-cloud miniapp, specifically from lines 2655 - 2658 of the file cloudsc.F90 (which contains a single ~ 2800 line long subroutine ![]() ):
):
! Backsubstitution
! step 1
DO JN=2,NCLV
DO JM = 1,JN-1
ZQXN(KIDIA:KFDIA,JN)=ZQXN(KIDIA:KFDIA,JN)-ZQLHS(KIDIA:KFDIA,JN,JM) &
& *ZQXN(KIDIA:KFDIA,JM)
ENDDO
ENDDO
Rewriting the array expression as a loop,
DO JM = 1,JN-1
DO JL = KIDIA, KFDIA
ZQXN(JL,JN) = ZQXN(JL,JN) - factor*ZQXN(JL,JM)
ENDDO
ENDDO
gives a loop nest resembling what is shown in the slide.
I just saw this talk today and I wondered the same thing…
I think the problem for auto-vectorization is that the compiler might not be able to deduce there is no aliasing, because the JM terminates at JN - 1, and the results are accumulated into column JN. One way to fix this would be using an IVDEP directive, or using an !$omp simd directive. Edit: do concurrent (DC) would also work (assuming the Fortran compiler sees DC as an IVDEP annotation and not some other parallelization mode).
A very similar problem occurs during the trailing panel update in LU factorization. Levesque & Williamson write about this in “A Guidebook to Fortran on Supercomputers”:
In the next few examples we will examine cases where the compiler may not know if a loop is recursive. Loop nest 42030 is a traditionally coded Gaussian elimination scheme. Most compilers will try to vectorize the inner loop where row subtraction is taking place. Note that
A(J,K)is a function ofA(J,I). Although bothIandJare fixed values within that inner loop a compiler must attempt to determine whetherKever assumes the value ofI(on other than the last iteration), since this would be recursive and must not be vectorized.There are two approaches for the compiler in optimizing this case. The first approach is to be smart enough to recognize that there is no possibility for recursion, since the initial (and lowest) value of
KisI+1. The other approach is to generate one code sequence for executing the loop in scalar mode and another sequence to execute it in vector mode, then test at runtime whetherKwill assume the value ofIin the inner loop. This second approach is called conditional compilation and is used quite extensively by CFT 1.15 [Cray Fortran].To assure that the compiler does fully vectorizes the restructured loop 42031 we have inserted directives (for Alliant, Cray, and NEC in this case) that inform the compiler to ignore potential recursion within the loop. Figure 4.10 illustrates that the performance improves by 50-100% for longer vector lengths. The performance gain results from the elimination of the execution time test by the compiler.
C THE ORIGINAL
C GAUSS ELIMINATION
DO 43020 I = 1, MATDIM
A(I,I) = 1. / A(I,I)
DO 43020 J = I+1, MATDIM
A(J,I) = A(J,I) * A(I,I)
DO 43020 K = I+1, MATDIM
A(J,K) = A(J,K) - A(J,I) * A(I,K)
43020 CONTINUE
C THE RESTRUCTURED
C GAUSS ELIMINATION
DO 43021 I = 1, MATDIM
A(I,I) = 1. / A(I,I)
DO 43021 J = I+1, MATDIM
A(J,I) = A(J,I) * A(I,I)
CVD$ NODEPCHK
CDIR$ IVDEP
*VDIR NODEP
DO 43021 K = I+1, MATDIM
A(J,K) = A(J,K) - A(J,I) * A(I,K)
43021 CONTINUE
I wrote fortran code for all of those machines in the 1980s and early 1990s, and I used those same compiler directives many times.
I think is this case, a slight rewrite of the code allows the compiler to vectorize the innermost loop.
DO 43020 I = 1, MATDIM
A(I,I) = 1. / A(I,I)
DO 43020 J = I+1, MATDIM
AJI = A(J,I) * A(I,I)
A(J,I) = AJI
DO 43020 K = I+1, MATDIM
A(J,K) = A(J,K) - AJI * A(I,K)
43020 CONTINUE
The compiler will likely not even store the AJI variable in memory, it will just live in a register for its lifetime. Of course, one would like for a fortran compiler to recognize all cases of vectorization, or the lack of recursion in this case, but especially in the 1980s that did not always occur. However, if this is still the situation in the language almost 40 years later, perhaps there should be some standard way to tell the compiler what to do.
do concurrent? Array expressions?
!$omp simd also belongs to a standard. If I remember correctly, the Intel Fortran compiler has -qopenmp-simd turned ON by default.
The compiler would need to prove that I+1 .. MATDIM and I are disjoint sets, hence the loop can be safely vectorized. I guess there is a name for this type of reasoning (loop aliasing analysis?). Maybe @certik knows?
Here is a slight variation of Levesque’s loop and the DGER routine:
subroutine trailing_update(m,n,A,lda,k)
integer, parameter :: dp = kind(1.0d0)
integer, intent(in) :: m, n, lda, k
real(dp), intent(inout) :: A(lda,n)
integer :: i, j
do j = k+1,n
do i = k+1,m
A(i,j) = A(i,j) - A(i,k)*A(k,j)
end do
end do
end subroutine
When compiling with gfortran -O2 -ftree-vectorize -march=skylake, it creates both a scalar and a vector path (just like Cray CFT did):
If you add !GCC$ IVDEP or !$omp simd the scalar path dissappears:
Even the Intel compiler (ifx -O3 -xSKYLAKE) struggles to create a vector version. Instead it unrolls 4 iterations and uses scalar instructions:
.LBB0_5:
vmovsd xmm0, qword ptr [r13 + 8*rsi - 8]
vmovsd xmm1, qword ptr [r11 + rbp - 24]
vfnmadd213sd xmm1, xmm0, qword ptr [r14 + rbp - 24]
vmovsd qword ptr [r14 + rbp - 24], xmm1
vmovsd xmm0, qword ptr [r13 + 8*rsi - 8]
vmovsd xmm1, qword ptr [r11 + rbp - 16]
vfnmadd213sd xmm1, xmm0, qword ptr [r14 + rbp - 16]
vmovsd qword ptr [r14 + rbp - 16], xmm1
vmovsd xmm0, qword ptr [r13 + 8*rsi - 8]
vmovsd xmm1, qword ptr [r11 + rbp - 8]
vfnmadd213sd xmm1, xmm0, qword ptr [r14 + rbp - 8]
vmovsd qword ptr [r14 + rbp - 8], xmm1
vmovsd xmm0, qword ptr [r13 + 8*rsi - 8]
vmovsd xmm1, qword ptr [r11 + rbp]
vfnmadd213sd xmm1, xmm0, qword ptr [r14 + rbp]
vmovsd qword ptr [r14 + rbp], xmm1
add rbp, 32
cmp r15, rbp
jne .LBB0_5
When you add !dir$ ivdep or !$omp simd, then ifx also does the right thing:
vbroadcastsd ymm1, xmm0
xor ebx, ebx
.LBB0_7:
vmovupd ymm2, ymmword ptr [r9 + 8*rbx]
vfnmadd213pd ymm2, ymm1, ymmword ptr [r10 + 8*rbx]
vmovupd ymmword ptr [r10 + 8*rbx], ymm2
add rbx, 4
cmp rbx, r8
jb .LBB0_7
One more difference worthy of notice, ![]() the Intel compiler broadcasts the
the Intel compiler broadcasts the A(k,j) value before the hot loop . ![]()
gfortran does the scalar-to-vector broadcast on each iteration (despite the fact that rax is constant in that loop).
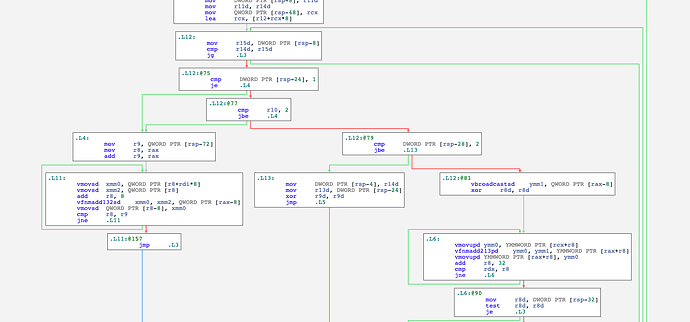
What is interesting is IFORT vectorizes this loop nest even without directives:
..B1.14: # Preds ..B1.12 ..B1.10
vbroadcastsd ymm3, xmm1 #10.38
vbroadcastsd ymm2, xmm0 #10.38
movsxd rcx, esi #9.9
mov r8, QWORD PTR [-48+rsp] #9.9[spill]
..B1.15: # Preds ..B1.15 ..B1.14
vmovupd ymm4, YMMWORD PTR [r8+rdx*8] #10.31
vfnmadd213pd ymm4, ymm3, YMMWORD PTR [rbx+rdx*8] #10.13
vmovupd YMMWORD PTR [rbx+rdx*8], ymm4 #10.13
vmovupd ymm5, YMMWORD PTR [r8+rdx*8] #10.31
vfnmadd213pd ymm5, ymm2, YMMWORD PTR [rdi+rdx*8] #10.13
vmovupd YMMWORD PTR [rdi+rdx*8], ymm5 #10.13
vmovupd ymm6, YMMWORD PTR [32+r8+rdx*8] #10.31
vfnmadd213pd ymm6, ymm3, YMMWORD PTR [32+rbx+rdx*8] #10.13
vmovupd YMMWORD PTR [32+rbx+rdx*8], ymm6 #10.13
vmovupd ymm7, YMMWORD PTR [32+r8+rdx*8] #10.31
vfnmadd213pd ymm7, ymm2, YMMWORD PTR [32+rdi+rdx*8] #10.13
vmovupd YMMWORD PTR [32+rdi+rdx*8], ymm7 #10.13
vmovupd ymm8, YMMWORD PTR [64+r8+rdx*8] #10.31
vfnmadd213pd ymm8, ymm3, YMMWORD PTR [64+rbx+rdx*8] #10.13
vmovupd YMMWORD PTR [64+rbx+rdx*8], ymm8 #10.13
vmovupd ymm9, YMMWORD PTR [64+r8+rdx*8] #10.31
vfnmadd213pd ymm9, ymm2, YMMWORD PTR [64+rdi+rdx*8] #10.13
vmovupd YMMWORD PTR [64+rdi+rdx*8], ymm9 #10.13
vmovupd ymm10, YMMWORD PTR [96+r8+rdx*8] #10.31
vfnmadd213pd ymm10, ymm3, YMMWORD PTR [96+rbx+rdx*8] #10.13
vmovupd YMMWORD PTR [96+rbx+rdx*8], ymm10 #10.13
vmovupd ymm11, YMMWORD PTR [96+r8+rdx*8] #10.31
vfnmadd213pd ymm11, ymm2, YMMWORD PTR [96+rdi+rdx*8] #10.13
vmovupd YMMWORD PTR [96+rdi+rdx*8], ymm11 #10.13
add rdx, 16 #9.9
cmp rdx, rcx #9.9
jb ..B1.15 # Prob 82%
Roughly speaking it interleaves the updates for two iterations in the second dimension (notice the vbroadcastsd), and unrolling 16 iterations along the first array dimension. It also uses different registers, presumably to avoid (false) instruction scheduling dependencies. I wonder what heuristics it uses to determine these unrolling factors. Obviously register availability is one.
ifx does something similar as IFORT, when you use
do concurrent (j = k+1:n, i=k+1:m)
A(i,j) = A(i,j) - A(i,k)*A(k,j)
end do
But instead of chunks 16 x 2, it iterates across chunks of size 4 x 8. Also note the repeates use of ymm0:
vmovapd xmmword ptr [rsp + 48], xmm8
vbroadcastsd ymm8, xmm8
vbroadcastsd ymm9, xmm1
vbroadcastsd ymm10, xmm2
vbroadcastsd ymm11, xmm3
vbroadcastsd ymm12, xmm4
vbroadcastsd ymm13, xmm5
vbroadcastsd ymm14, xmm6
vbroadcastsd ymm15, xmm7
xor eax, eax
.LBB0_9:
vmovupd ymm0, ymmword ptr [rbp + 8*rax]
lea rdx, [r11 + 8*rax]
vfnmadd213pd ymm0, ymm8, ymmword ptr [r11 + 8*rax]
vmovupd ymmword ptr [r11 + 8*rax], ymm0
vmovupd ymm0, ymmword ptr [rbp + 8*rax]
vfnmadd213pd ymm0, ymm9, ymmword ptr [rcx + rdx]
vmovupd ymmword ptr [rcx + rdx], ymm0
add rdx, rcx
vmovupd ymm0, ymmword ptr [rbp + 8*rax]
vfnmadd213pd ymm0, ymm10, ymmword ptr [rcx + rdx]
vmovupd ymmword ptr [rcx + rdx], ymm0
lea rdx, [rdx + rcx]
vmovupd ymm0, ymmword ptr [rbp + 8*rax]
vfnmadd213pd ymm0, ymm11, ymmword ptr [rcx + rdx]
vmovupd ymmword ptr [rcx + rdx], ymm0
lea rdx, [rdx + rcx]
vmovupd ymm0, ymmword ptr [rbp + 8*rax]
vfnmadd213pd ymm0, ymm12, ymmword ptr [rcx + rdx]
vmovupd ymmword ptr [rcx + rdx], ymm0
lea rdx, [rdx + rcx]
vmovupd ymm0, ymmword ptr [rbp + 8*rax]
vfnmadd213pd ymm0, ymm13, ymmword ptr [rcx + rdx]
vmovupd ymmword ptr [rcx + rdx], ymm0
add rdx, rcx
vmovupd ymm0, ymmword ptr [rbp + 8*rax]
vfnmadd213pd ymm0, ymm14, ymmword ptr [rcx + rdx]
vmovupd ymmword ptr [rcx + rdx], ymm0
add rdx, rcx
vmovupd ymm0, ymmword ptr [rbp + 8*rax]
vfnmadd213pd ymm0, ymm15, ymmword ptr [rcx + rdx]
vmovupd ymmword ptr [rcx + rdx], ymm0
add rax, 4
cmp rax, r13
jbe .LBB0_9
So three compilers, three different strategies. Two compilers (gfortran and ifx) only vectorize when the programmer asserts it is safe.
Addendum: gfortran moves the broadcast before the loop if written like @RonShepard suggested:
do j = k+1,n
tmp = A(k,j)
do i = k+1,m
A(i,j) = A(i,j) - A(i,k)*tmp
end do
end do
vbroadcastsd ymm1, xmm2
xor edi, edi
.L6:
vmovupd ymm0, YMMWORD PTR [rcx+rdi]
vfnmadd213pd ymm0, ymm1, YMMWORD PTR [rax+rdi]
vmovupd YMMWORD PTR [rax+rdi], ymm0
add rdi, 32
cmp rdx, rdi
jne .L6
The iteration space is traversed in chunks of 4 x 1, same as ifx did.
This is obvious to a human, but I have no idea how optimizers deduce such things, or whether this is part of the language-specific front end or part of the general back end of a modern compiler.
I did think about do concurrent, but my feeling is that construct is more about concurrent stripmining and subblocking that it is about recursion. However, the lack of recursion is indeed part of the semantics of that construct, so maybe that is sufficient? I also considered OpenMP, and I think that also works, but it implies multithreaded execution, which is also above and beyond just telling the compiler that no recursion is occurring within the loop. And, of course, OpenMP is not part of the language standard, it is a separate standard. Array syntax actually does the opposite of what the programmer needs; it tells the compiler if it can’t figure it out, then allocate temporary arrays for the operands and for the result and do everything with those temporary arrays. In this case, with just two floating point operations per loop cycle that workspace allocation and data movement would be a performance disaster.
Thanks much for your effort within compiler explorer. I don’t understand the details of the machine instructions, but I think I can follow your discussion and understand the consequences of the various compiler choices.
I don’t know either yet. After beta we’ll focus on optimizations more with LFortran. I have many ideas though. ![]()
IIRC, CFT 1.14 could also do it. At the time, Cray was also developing the next generation compiler - CFT77. There was a period where CFT could do tricks that CFT77 couldn’t - and vice versa. CFT77 was a globally optimizing compiler, whereas CFT mostly optimized within basic blocks, and towards the end, extended basic blocks. So CFT77 generated better scalar code from the start. But eventually CFT77 learned all of CFT’s vector tricks.
What was really fun was when one of the compiler developers grafted the C compiler front end onto the CFT77 optimization/vectorization and code generation. It was one of those little “after midnight” projects which worked a little too well, and ended up causing a bit of a stir…